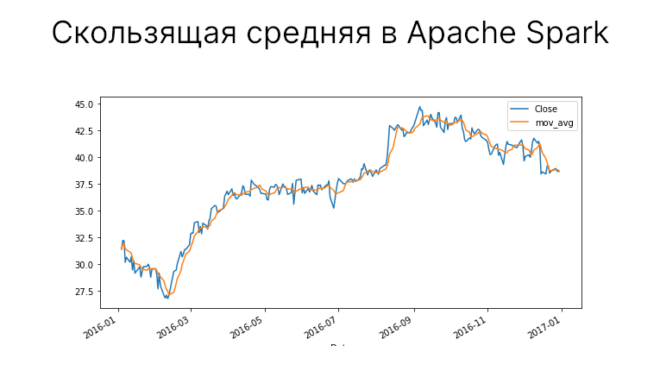
Скользящая средняя (moving average) часто применяется для анализа и определения трендов в данных. Она рассчитывается как среднее текущего и заданного числа предыдущих значений за некоторый период. На этом основании можно узнать, как ведет себя среднее значение с течением времени. В этой статье разберемся, как найти скользящую среднюю в PySpark, а также, как построить графики с помощью Pandas.
Данные с биржи и переход от PySpark к Pandas
Для примера возьмем датасет с данными об акциях. Мы даже использовали этот датасет в статье по визуализации временных рядов. Вы можете скачать датасет из нашего репозитория.
df_sp = spark.read.csv("stock_data.csv", header=True)
"""
+--------+-----+-----+-----+-----+--------+----+
| Date| Open| High| Low|Close| Volume|Name|
+--------+-----+-----+-----+-----+--------+----+
|1/3/2006|39.69|41.22|38.79|40.91|24232729|AABA|
|1/4/2006|41.22| 41.9|40.77|40.97|20553479|AABA|
|1/5/2006|40.93|41.73|40.85|41.53|12829610|AABA|
|1/6/2006|42.88|43.57| 42.8|43.21|29422828|AABA|
|1/9/2006| 43.1|43.66|42.82|43.42|16268338|AABA|
+--------+-----+-----+-----+-----+--------+----+
"""
Построим график цены закрытия за 2016 год. Для этого нам придется преобразовать датафрейм PySpark в датафрейм Pandas, потому что в PySpark отсутствует возможность проводить визуализацию.
Переход из PySpark в Pandas — достаточно дорогая операция. Но, к счастью, датасет небольшой, и мы также проведем фильтрацию. В итоге в фильтрованных данных всего 252 строки. Также распарсим столбец с датами и сделаем его в виде индекса. Код на Python:
import pandas as pd
df_sp_2016 = df_sp \
.filter("Date like '%/%/2016'") \
.select("Date", "Close")
df_pd = df_sp_2016.toPandas()
df_pd["Date"] = pd.to_datetime(df_pd["Date"], format='%m/%d/%Y')
df_pd.set_index("Date", inplace=True)
Теперь мы можем очень просто построить график зависимости даты от цены закрытия. В одной из наших статей мы говорили о том, как строить графики в Pandas. Пример кода на Python:
df_pd.plot(y="Close", use_index=True, figsize=(10, 5))
Что такое скользящая средняя
Скользящая средняя для каждой временной точки считается, как среднее арифметическое между текущим значением и предыдущих. Причем количество предыдущих выбирается нами. Например, рассмотрим два предыдущих, тогда для нашего датасета скользящая средняя будет:
+---------+-----+ | Date|Close| +---------+-----+ | 1/4/2016|31.40| = 31.4 | 1/5/2016|32.20| = (32.2 + 31.4) / 2 = 31.8 | 1/6/2016|32.16| = (32.16 + 32.20 + 31.40) / 3 = 31.92 | 1/7/2016|30.16| = (30.16 + 32.16 + 32.20) / 3 = 31.51 | 1/8/2016|30.63| = (30.63 + 30.16 + 32.16) / 3 = 30.98 +---------+-----+
У первого значения предыдущих нет, поэтому оно остается каким есть. У второго значения только одно предыдущее значение, поэтому рассчитывается среднее между ним и этим предыдущим, т.е. путем делением на два. А вот все остальные вплоть до самого последнего значения имеют по два предыдущих значения, поэтому средняя для них рассчитывается одинаково.
Если бы было окно из пяти строк, то первые четыре значения считались путем деления на 1, 2, 3 и 4. А остальные на 5. В этом и состоит суть скользящей средней.
Как найти скользящую среднюю в PySpark
С помощью оконных функций (window functions), о которых мы говорили в прошлой статье, сделать это очень просто. Нам нужно ли применить окно из N строк, которое состоит из текущей строки и N предыдущих. Это делается с помощью предложения rows between.
Запрос SQL для подсчета скользящей средней с окном из трех строк будет выглядеть так:
SELECT Date, Close,
AVG(Close) OVER(ROWS BETWEEN 2 PRECEDING AND CURRENT ROW)
as mov_avg
FROM stock_data;
А вот в самом Apache PySpark подсчет скользящей средней будет выглядеть так:
from pyspark.sql import Window
import pyspark.sql.functions as F
w = Window.rowsBetween(-2, Window.currentRow)
mov_avg = F.round(F.avg("Close").over(w), 3).alias("mov_avg")
df_sp_2016 = df_sp_2016.select("Date", "Close", mov_avg)
"""
+--------+-----+-------+
| Date|Close|mov_avg|
+--------+-----+-------+
|1/4/2016| 31.4| 31.4|
|1/5/2016| 32.2| 31.8|
|1/6/2016|32.16| 31.92|
|1/7/2016|30.16| 31.507|
|1/8/2016|30.63| 30.983|
+--------+-----+-------+
"""
Мы здесь добавили округление с помощью функции round, чтобы не выводить все цифры после запятой. Как видите, значения скользящей средней в точности совпадает с тем, что мы рассчитывали вручную.
Как построить скользящую среднюю в виде графика
Для построения графика нам все также понадобится перевести в датафрейм Pandas. Здесь нужно проделать те же самые шаги, что мы делали до этого:
df_pd = df_sp_2016.toPandas()
df_pd["Date"] = pd.to_datetime(df_pd["Date"], format='%m/%d/%Y')
df_pd.set_index("Date", inplace=True)
При построении графика нужно не забыть про второй столбец:
df_pd.plot(y=["Close", "mov_avg"], use_index=True, figsize=(10, 5))
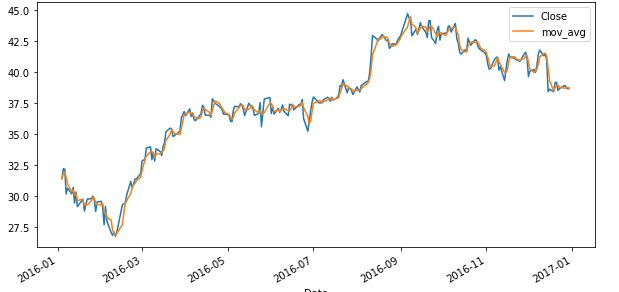
Оранжевая линия показывает скользящую среднюю. Ниже график уже с окном из пяти предыдущих значений (построенное тем же самым способом, но вместо значения -2 стоит -5). Как видим, она еще более глаже, чем предыдущая.
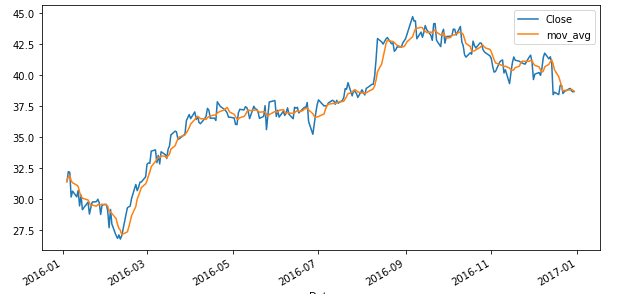
Подобным образом строятся графики на трейдинговых платформах (но, скорее всего, с помощью JavaScript, если это веб-сервис).
Код курса
MLSP
Ближайшая дата курса
по запросу
Продолжительность
ак.часов
Стоимость обучения
0 руб.
Еще больше подробностей о оконных и агрегатных функциях с их практическим применением вы узнаете на наших образовательных курсах в лицензированном учебном центре обучения и повышения квалификации руководителей и IT-специалистов (менеджеров, архитекторов, инженеров, администраторов, Data Scientist’ов и аналитиков Big Data) в Москве: