Продолжим говорить об алгоритмах машинного обучения Apache Spark. Сегодня рассмотрим метод опорных векторов. В этой статье вы узнаете, как решается задача классификации на примере реального датасета с помощью метода опорных векторов в Apache Spark.
Краткие сведения о принципе работы метода опорных векторов
Метод опорных векторов (support vector machine, SVM) — алгоритм классификации, в основе которого лежит определяемая разделяющая гиперплоскость (линия, прямая, многомерные плоскости). Другими словами, при заданных тренировочных данных алгоритм находит такую гиперплоскость, которая разделяет данные, принадлежащие разным классам, самым оптимальным способом. В двухмерном пространстве гиперплоскостью служит прямая линия (см. рис. ниже).
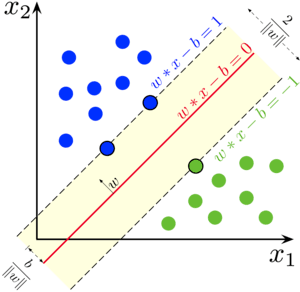
Точки, которые стоят ближе всего к гиперплоскости называются опорными векторами, а расстояние от этих векторов до гиперплоскости называется зазором. Чем дальше опорные вектора отстоят от гиперплоскости, тем больше вероятность правильной классификации. Может случиться так, что несколько точек 1-го класса лежат в области 2-го. Тогда зазор окажется маленьким, и может возникнуть переобучение. Чтобы это предотвратить, SVM игнорирует такие случаи путем их подсчета на основе кросс-валидации. Таким образом, точки, оказавшиеся внутри зазора игнорируются (считаются классифицированными неверно).
В Apache Spark реализован линейный классификатор опорных векторов (linear support vector classifier). Его следует использовать только тогда, когда данные определяются как на рисунке выше. Для нелинейных отношений лучше было бы использовать SVM с ядерной функцией, но такого в Apache Spark нет. В этом случае воспользуйтесь деревьями решений (о них тут).
Метод опорных векторов в Apache Spark: примеры кода
Модуль ML имеет класс LinearSVC, который отвечает за реализацию метода опорных векторов [1]. Он проводит только бинарную классификацию (когда классов два). Функция потерь — hinge loss [2] с оптимизатором OWLQN [3]; поддерживается только L2-регуляризацию.
В качестве датасета воспользуемся данными о кредитовании. Каждая запись представляет человека, которому можно дать кредит (creditability=1) или нельзя (creditability=0) на основании его личных данных, например, зарплате, возрасте, семейном положении и т.д. Датасет располагается в нашем репозитории. Итак, в первую очередь прочитаем его:
df = spark.read.csv("credit.csv", inferSchema=True, header=True)
## Некоторые из столбцов
+-------------+---+------+----------+
|creditability|age|amount|sexMarried|
+-------------+---+------+----------+
| 1| 21| 1049| 2|
| 1| 36| 2799| 3|
| 1| 23| 841| 2|
| 1| 39| 2122| 3|
| 1| 38| 2171| 3|
+-------------+---+------+----------+
only showing top 5 rows
Далее, нам требуется векторизовать признаки. В Apache Spark делается это с помощью класса VectorAssembler. Векторизованные признаки назовем features. Также предварительно разобьем датасет на тренировочную и тестовую выборки в отношении 8:2 с помощью метода randomSplit.
Код для векторизации признаков и разбиения на выборки в Apache Spark выглядит следующим образом:
from pyspark.ml.feature import VectorAssembler
assembler = VectorAssembler(
inputCols=["amount", "savings", "assets", "age", "credits"],
outputCol="features"
)
output = assembler.transform(df)
train, test = output.randomSplit([0.8, 0.2])
Обучение метода опорных векторов Apache Spark
На тренировочной выборки обучим метод опорных векторов. Как уже было сказано, для этого используется класс ‘LinearSVC’. Он принимает следующие параметры [4]:
featuresCol— столбец с векторизованными признаками (по умолчаниюfeatures);labelCol— целевой столбец, класс которого нужно определить (по умолчаниюlabel);regParam— параметр регуляризации, который определяет насколько сильно нужно игнорировать данные, попавшие в зазор (по умолчанию 0);fitIntercept— нужно ли рассчитывать точку пересечения (по умолчаниюTrue).
Для нашего конкретного случая обязательно нужно указать labelCol, так как целевой столбец имеет название creditability. Обучение осуществляется вызовом метода fit.
Итак, пример кода для обучения метода опорных векторов в Apache Spark выглядит так:
from pyspark.ml.classification import LinearSVC
lsvc = LinearSVC(labelCol="creditability",
regParam=0.1)
model = lsvc.fit(train)
Мы можем посмотреть получившиеся коэффициента (признаков всего 5, следовательно, коэффициентов тоже 5):
print("Coefficients:", model.coefficients)
print("Intercept:", model.intercept)
## Результаты:
Coefficients: [-3.97e-08,7.61e-05,-0.00e-06,-5.23e-06]
Intercept: 1.00039
Очень малые коэффициенты говорят нам о том, что они практические не влияют на итоговую модель. Если признаков было бы всего два, то гиперплоскостью являлось бы прямая линия, параллельная оси абсцисс.
Для получения прогнозов на тестовой выборке вызывается метод transform, который в качестве аргумента принимает эту самую выборку. А для того чтобы оценить точность модели воспользуемся классом BinaryClassificationEvaluator, поскольку у нас бинарная классификация. В нем также нужно указать целевой столбец:
from pyspark.ml.evaluation import BinaryClassificationEvaluator ev = BinaryClassificationEvaluator(labelCol="creditability") accuracy = ev.evaluate(predictions) print(f"Test Error =", accuracy) # Результат: Test Error = 0.681
Еще больше подробностей о алгоритмах машинного обучения, в том числе и методе опорных векторов, вы узнаете на специализированном курсе по машинному обучению «Потоковая обработка данных» в лицензированном учебном центре обучения и повышения квалификации разработчиков, менеджеров, архитекторов, инженеров, администраторов, Data Scientist’ов и аналитиков Big Data в Москве.
- https://spark.apache.org/docs/latest/ml-classification-regression.html#linear-support-vector-machine
- https://en.wikipedia.org/wiki/Hinge_loss
- https://www.microsoft.com/en-us/download/details.aspx?id=52452
- https://spark.apache.org/docs/latest/api/python/reference/api/pyspark.ml.classification.LinearSVC.html