Деревья решений (Decision trees) являются одним из самых популярных алгоритмов машинного обучения и используются для задач классификации (бинарной и многоклассовой) и регрессии. Деревья решений простоты, понятны, они хорошо обрабатывают категориальные значения, а также могут находить нелинейные связи. В этой статье вы узнаете о реализации деревьев решений в Spark MLlib, мере узловой неопределенности (impurity) в классификации и регрессии с примерами кода на Python.
Реализация деревьев решений в Spark MLlib
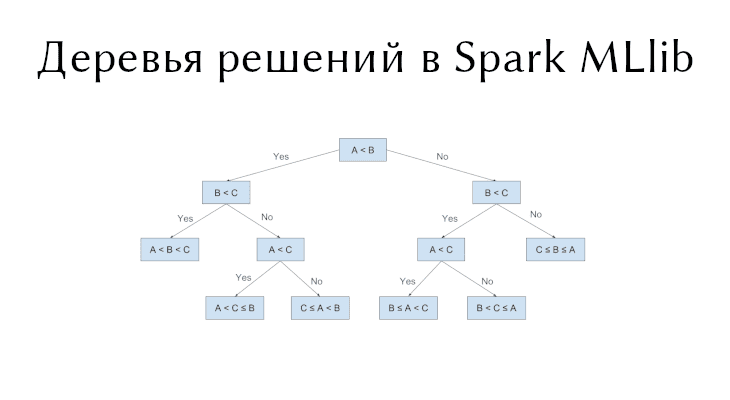
Дерево решений – это жадный алгоритм, который выполняет рекурсивное двоичное разбиение пространства признаков, т.е. имеется один родитель и два потомка. Дерево предсказывает один и тот же класс каждого последнего узла. Жадный выбор падает на наилучшее разбиение из набора возможных разбиений, чтобы получить максимальную информационную ценность. Другими словами, разбиение, сделанное в каждом узле дерева, выбирается из набора argmax[IG(D, s)], где IG(D, s) – это информационный ценность разбиения s, примененное к набору данных D.
Мера узловой неопределенности и информационная ценность
Мера узловой неопределенности (Node impurity) – это мера однородности классов в узле. Apache Spark предлагает два метода измерения неопределенности для классификации (коэффициент Джини и энтропия) и один метод для регрессии (отклонение).
| Неопределенность | Задача | Формула | Описание |
|---|---|---|---|
| Коэффициент Джини | Классификация | f_i – частота класса i в узле, C – количество уникальных классов | |
| Энтропия | Классификация | f_i – частота класса i в узле, C – количество уникальных классов | |
| Отклонение | Регрессии | y_i – класс экземпляра, N – количество экземпляров, mu – среднее (сумма всех y_i, деленное на N ) |
Информационная ценность – это разность между родительским узлом и суммой весов двух следующих потомков. Предполагая, что разбиение s разделяет датасет D размера N на два датасета D_left и D_right с размерами N_left и N_right соответственно, информационная ценность определяется как:
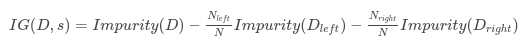
Кандидаты на разбиение: непрерывные и категориальные значения
При непрерывных значениях кандидатами на разбиение являются все уникальные значения этого признака. Некоторые реализации предварительно сортируют значения, а затем используют упорядоченные уникальные значения в качестве кандидатов на разбиение для более быстрых расчетов дерева.
Сортировка значений для больших распределенных наборов данных требует очевидно больших затрат. Эта реализация вычисляет приблизительный набор кандидатов на разбиение, выполняя расчет квантилей по отобранной части данных. Упорядоченные разбиения создают бины (bins), и их максимальное количество можно указать с помощью параметра maxBins.
Заметим, что количество бинов не может быть больше количества экземпляров N (такое редко случается, поскольку значение maxBins по умолчанию равно 32). Алгоритм автоматически уменьшит их количество, если условие не выполняется.
Для категориальных признаков с M возможными категориями можно было получить 2^(M−1) − 1 кандидатов на разбиение. Для регрессии и бинарной классификации можно уменьшить количество кандидатов до M-1, упорядочив значения категориальных признаков по количеству значений каждой категории. Например, для задачи бинарной классификации с одним категориальным признаком, у которого три уникальных значения A, B и C, заданных в пропорции 0.2, 0.6 и 0.4, они будут упорядочены вот так: A, C, B. Двумя кандидатами на разбиение являются A|C, B и A, C|B, где | обозначает разбиение.
В многоклассовой классификации используются все возможные разбиения 2^(M-1)-1, когда это возможно. Когда эта комбинация больше параметра maxBins, используется эвристический метод, аналогичный методу, используемому для двоичной классификации и регрессии. M категориальных признаков сортируются по мере неопределенности, а затем рассматриваются результирующие M-1 кандидатов.
Правило останова и его критерии
Рекурсивное построение дерева останавливается на узле, когда выполняется одно из следующих условий:
- Глубина узла равна параметру обучения
maxDepth. - Отсутствие кандидата на разбиение приводит к значению информационной ценности, которое превышает
minInfoGain. - Ни один из кандидатов на разбиение не создает дочерние узлы, каждый из которых имеет как минимум обучающие экземпляры
minInstancesPerNode.
Приведенные параметры определяют, когда дерево перестанет строиться (добавляться новые узлы). При настройке этих параметров будьте осторожны при валидации тестовых данных, чтобы избежать переобучения.
maxDepth– максимальная глубина дерева. Глубокие деревья потенциально обеспечивают более высокую точность, но их дольше обучать и они с большей вероятностью переобучатся.minInstancesPerNode– минимальное количество обучающих экземпляров на узел. Для дальнейшего разбиения узла каждый из его дочерних узлов должен иметь по крайней мере это количество. Данный параметр обычно используется с RandomForest, поскольку этот алгоритм более “глубокий”.minInfoGain– минимальная информационная ценность.
Пример деревьев решений в Spark MLlib
В примере покажем, как загрузить данные в формате LIBSVM [1], представить их в виде RDD из LabeledPoint (о нем тут), а затем как выполнить классификацию с использованием дерева решений с коэффициентом Джини в качестве меры неопределенности и максимальной глубиной дерева равной 5. Ошибка модели вычисляется для измерения точности алгоритма.
В первую очередь загрузим данные из официального репозитория Apache Spark. Для чтение данных формате LIBSVM используется модуль MLUtils. Затем прочитанный датасет разделим на обучающую и тестовую выборки в пропорции 7:3 соответственно через randomSplit.
Код на Python для чтения данных в Apache Spark и их разбиения на отдельные выборки выглядит следующим образом:
from pyspark.mllib.tree import DecisionTree, DecisionTreeModel from pyspark.mllib.util import MLUtils # sc: экземляр SparkContext data = MLUtils.loadLibSVMFile(sc, 'data/mllib/sample_libsvm_data.txt') trainingData, testData = data.randomSplit([0.7, 0.3])
Чтобы обучить деревья решений Apache Spark в рамках классификации, используется метод trainClassifier. Приведенные данные не имеют категориальных признаков, поэтому параметр categoricalFeaturesInfo – пустой.
model = DecisionTree.trainClassifier(
trainingData, numClasses=2, categoricalFeaturesInfo={},
impurity='gini', maxDepth=5, maxBins=32)
Осталось вызвать метод predict, который при передаче в качестве аргумента тестовых данных возвращает предсказанные классы/метки. Ошибку модели посчитаем как отношение количества неправильных ответов к общему количеству записей.
Пример кода для получения предсказаний и подсчета ошибки модели машинного обучения Spark MLlib выглидт так:
predictions = model.predict(testData.map(lambda x: x.features))
labelsAndPredictions = testData.map(lambda lp: lp.label).zip(predictions)
testErr = labelsAndPredictions.filter(
lambda lp: lp[0] != lp[1]).count() / float(testData.count())
print('Test Error = ' + str(testErr))
print('Learned classification tree model:')
print(model.toDebugString())
Для решения задачи регрессии используется метод trainRegressor, где по умолчанию мера неопределенности равна variance, поэтому получилось бы тогда вот так (остальной код такой же):
model = DecisionTree.trainRegressor(
trainingData, categoricalFeaturesInfo={},
maxDepth=5, maxBins=32)
О том как проводить обучение различных моделей, в том числе деревьев решений, и о том как их применять на реальных примерах Data Science вы узнаете на специализированном курсе по машинному обучению «Машинное обучение в Apache Spark» в лицензированном учебном центре обучения и повышения квалификации разработчиков, менеджеров, архитекторов, инженеров, администраторов, Data Scientist’ов и аналитиков Big Data в Москве.