В рамках анализа данных и отбора признаков нередко вычисляется корреляция между признаками. Сегодня мы разберем, что такое корреляция, какие методы вычисления существуют, как найти коэффициенты Пирсона и Спирмена, а также как построить матрицу корреляция в Spark.
Что такое корреляция
Корреляция — эта статистическая взаимосвязь двух случайных переменных. С ростом или падением значений одной переменной изменяются значения и другой перемнной. Например, с увеличением роста человека увеличивается его масса. В этом утверждении наблюдается связь между ростом и массой человека. Для подсчета этой связи и используется корреляция. А в численном виде она выражается через коэффициент корреляции. Но есть несколько способов расчета коэффициента корреляции, например, с помощью методов Пирсона (Pearson) и Спирмана (Spearman).
Коэффициент корреляции Пирсона считается как отношение ковариации переменных к произведению их отклонений. Ковариация — мера совместной изменчивости двух случайных величин. В отличие от корреляции не показывает насколько переменные объясняет друг друга, но указывает только на тренд, а также не имеет предельных значений. Ковариация равная 100 не значит, что это набор данных лучше, чем в в наборе данных с ковариацией 10 (мы можешь лишь сказать только то, что наблюдается положительный тренд в обоих случаях). Поэтому вместо ковариации и используется корреляция, однако она может применяться в методе главных компонент, о котором говорили тут.
На языке Python коэффициент корреляция Пирсона выражается очень просто:
def cov(x, y):
# Ковариация
N = len(x) - 1
dx = x - x.mean()
dy = y - y.mean()
return sum(dx * dy) / N
def std(x):
# Стандартное отклонение
N = len(x) - 1
ddx = (x - x.mean())**2
return np.sqrt(sum(ddx) / N)
corr = cov(X, Y) / (std(X) * std(Y))
Коэффициент корреляции Спирмана считается как отношение ковариации рангов переменных к произведению их отклонений. Для подсчета ранга переменной применяется следующая процедура: минимальному значению приравнивается ранг 1, следующему после него 2 и так до максимального значения. В Python, пользуясь функциями выше, коэффициент корреляции Спирмана может выражаться так:
from scipy.stats import rankdata
def rank(x):
# Исходный массив [4, 5, 0, 3]
# Его ранг: [3, 4, 1, 2]
return rankdata(x)
ran_a = rank(a)
ran_b = rank(b)
cov(ran_a, rank_b) / (std(rank_a) * std(rank_b))
В отличие от корреляции Пирсона, корреляция Спирмена не предполагает, что оба набора данных нормально распределены. В Википедии приведены рисунки, которые показывают различия между коэффициентами при одном наборе данных.
На основе значений коэффициента корреляции можно рассчитать насколько зависимы друг от друга переменные. Его значение находится в отрезке [-1, 1]. Если коэффициент корреляции близится к 0, то зависимость между переменными также стремится к нулю. Следовательно, изменение одной переменной не объясняет изменение второй.
Значение стремящееся к 1 показывает, что наблюдается положительный тренд, переменные объясняют друг друга. На графике это бы выглядело как в одну линию строятся точки.
Значение стремящееся к -1 показывает, что наблюдается отрицательный тренд, переменные объясняют друг друга. Но это уже склон вниз.
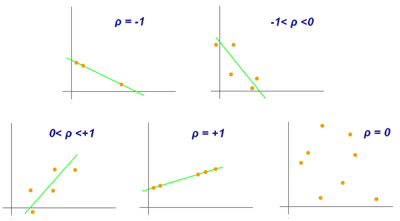
Исходя из значения коэффициента корреляции, можно сделать вывод о пригодности использования алгоритма машинного обучения — линейной регрессии. Ведь если он будет находиться около 1 или -1, то и линейную регрессию можно построить.
Матрица корреляции в Spark
Как уже сказано, подсчет корреляции производится для двух переменных. Поэтому для датасетов с более чем двумя признаками строится матрица корреляции — это матрица, показывающая значение коэффициентов корреляции для всех возможных пар признаков. Вот и в Spark матрицу корреляции можно рассчитать. Для этого используется класс Correlation из модуля ml.stat.
Допустим у нас имеется датасет в виде датафрейма Spark, ниже показан код для инициализации. Обратите внимание, что данные должны быть представлены в векторном виде, о том, как их преобразовать в векторы говорим тут
from pyspark.ml.linalg import Vectors
from pyspark.ml.stat import Correlation
data = [
(Vectors.dense([2.0, 0.0, 3.0, 4.0, 5.0]),),
(Vectors.dense([4.0, 0.0, 0.0, 6.0, 7.0]),),
(Vectors.dense([8.0, 1.0, 4.0, 9.0, 0.0]),),
(Vectors.dense([4.0, 5.0, 0.0, 3.0, 5.0]),),
(Vectors.dense([6.0, 7.0, 0.0, 8.0, 4.5]),),
]
df = spark.createDataFrame(data, ["features"])
>>> df.show(truncate=False) +---------------------+ |features | +---------------------+ |[2.0,0.0,3.0,4.0,5.0]| |[4.0,0.0,0.0,6.0,7.0]| |[8.0,1.0,4.0,9.0,0.0]| |[4.0,5.0,0.0,3.0,5.0]| |[6.0,7.0,0.0,8.0,4.5]| +---------------------+
Способ вычисления корреляции между парами признаков задается параметром method. В него можно передать значение pearson или spearman (по умолчанию стоит pearson). Тогда матрица корреляция, где коэффициенты найдены по методу Пирсона, в Spark выглядит так:
r1 = Correlation.corr(df, "features").head()
print("Pearson correlation matrix:\n" + str(r1[0]))
Pearson correlation matrix:
DenseMatrix([[ 1. , 0.259, 0.247, 0.860, -0.770],
[ 0.259, 1. , -0.567, 0.061, 0.018],
[ 0.247, -0.567, 1. , 0.301, -0.748],
[ 0.860, 0.061, 0.301, 1. , -0.606],
[-0.770, 0.018, -0.748, -0.606, 1. ]])
А вот матрица корреляции с коэффициентами, найденным по методу Спирмана, в Spark уже принимает немного другие значения:
r2 = Correlation.corr(df, "features", "spearman").head()
print("Spearman correlation matrix:\n" + str(r2[0]))
Spearman correlation matrix:
densematrix([[ 1. , 0.552, 0.229, 0.820, -0.763],
[ 0.552, 1. , -0.344, 0.153, -0.552],
[ 0.229, -0.344, 1. , 0.447, -0.573],
[ 0.820, 0.153, 0.447, 1. , -0.666],
[-0.763, -0.552, -0.573, -0.666, 1. ]])
Итак, исходя из значений коэффициента и Пирсона (0.86), и Спирмена (0.82), можно сделать вывод, что между 1-м и 3-м признаками наблюдается положительный тренд, около которого можно построить линейную регрессию. Также высокие значение коэффициентов наблюдаются у 1-го и 4-го признаков, но здесь уже отрицательный тренд (значения -0.770 и -0.763).
Матрица корреляция поможет вам для анализа зависимостей между признаками. А о том, как интерпретировать результаты корреляции и на их основе строить модели машинного обучения в Spark вы узнаете на специализированном курсе «Анализ данных с Apache Spark» в лицензированном учебном центре обучения и повышения квалификации разработчиков, менеджеров, архитекторов, инженеров, администраторов, Data Scientist’ов и аналитиков Big Data в Москве.